Medical physicists are Bayesians?

A look at whether medical physics are Bayesians through the example of maintenance of certification (MOC).

Abstract: Though few will admit it, many physicists are Bayesians in at least some situations. This post discusses how the world looks through a Bayesian eye. This is accomplished through a concrete example, the Maintenance of Certification (MOC) by the American Board of Radiology. It is shown that a priori acceptance of the value of MOC relies on a Bayesian attitude towards the meaning of probabilities. Applying Bayesian statistics, it is shown that a reasonable prior greatly reduces any possible gain in information by going through the MOC, as well as providing some numbers on the possible error rate of the MOC. It is hoped that this concrete example will result in a greater understanding of the Bayesian approach in the medical physics environment.

Introduction:

For several decades, a debate has raged regarding the nature of probabilities. On one side of the debate are “frequentists”. They hold that probabilities are obtained by repeated identical observations with the probability of any given outcome being the ratio of the number of events with that outcome to the total number of events. The classical example is the probability of observing a “heads” or “tails” when flipping a coin. On the other side of the debate are “Bayesians” (more on that name in a bit). They hold that probabilities can also represent the degree of belief in relative frequency of a given outcome. While there are many paths by which one can reach this point, there are several common ones. The influence of prior knowledge on one’s belief that a certain event will happen is certainly one ingredient. Another path by which people reach the Bayesian viewpoint is recognition of the fact that probabilities are often useful even when it is impossible to reproduce precisely the situation so that multiple measurements can be made, such as in the field of medicine.

For those of us in the medical field, randomized controlled trials (RCT) are our effort to achieve the frequentist goal of measuring outcomes in identical situations. However, we are usually more interested in discovering the differences in probabilities for different situations, namely when an element of a therapeutic procedure has been changed. The frequentist approach lies behind the statistical tests that are used to determine whether our observations warrant the conclusion that the therapeutic modification has resulted in a true difference or not. In other words, the frequentist view is one in which seeks to determine whether the data observed are consistent with a given hypothesis. This is to be contrasted with the Bayesian view in which one seeks to determine the probability of a certain hypothesis given the data.

All of this still leaves us with the question: Why do we care whether medical physicists are Bayesians or frequentists? One good reason has been in the news recently, namely, personalized medicine. How will we ever obtain the required numbers of patients if everything is personal? Even if we take “personal” to mean harboring one or several (nearly) identical genes, recent developments are demonstrating that biological processes are nearly always the result of a large set of genes. In addition, the role of epigenetic factors reduces the homogeneity in any group selected for their genetic homogeneity.

In general, medical physicists tend to be a bit under-educated with respect to probabilities and statistics, especially in a medical environment. A very good reference for the Bayesian statistical approach is “Bayesian Approaches to Clinical Trials and Health-Care Evaluation” by DJ Speigelhalter et al. This post is a brief attempt to highlight some of the issues, but should be considered a very faint ghost of a complete discussion. To make it more concrete, I have looked at a specific situation.

ABR Maintenance of Certification

According to the ABR website, the MOC is valued “because it demonstrates your support for continuous quality improvement, professional development, and quality patient care.” Now there are many ways in which these universally respected activities can be demonstrated so the MOC process must have some particular quality that makes it worthwhile to warrant it special status. One possibility is that it is felt that the processes of the MOC increase the probability that a physicist will do a good job in her/his areas of practice. This seems to be a reasonable assumption since the ABR itself states that certification (a) “does NOT (emphasis in original) suggest special achievement in the field of medical physics”, and (b) “The certificate signifies that its holder, at the time of taking the examinations, intended to make the practice of medical physics his or her chief concern.” [http://www.theabr.org/ic-rp-landing] Given this modest testimonial, the notion that the MOC improves the probability of good medical physics performance seems generous. [Note added 19 Aug 2015: A letter published in IJROBP, 93(1): 209-210, 2015 provides some references that challenge the notion that the MOC achieves an improvement in care.]

Now that probability has been introduced, we can take up the question of Bayesian vs frequentist views. For a frequentist, to show that MOC changes the probability requires a counting of good and bad physicists before and after undergoing MOC. One approach would be to examine those physicists who were certified before MOC came into being and who have subsequently signed up to participate in MOC. Another approach would be to examine concurrently those who are participating in MOC and those who are not. This could be accomplished by looking at those who were certified pre-MOC and who have not signed up. It might be difficult with this approach to avoid selection bias with respect to experience. Alternatively, one could find physicists practicing in countries without MOC. Finally, an RCT could be conducted in which newly certified physicists were randomly assigned to MOC or not. Assuming that the degradation of practice occurs at a pace no greater than the MOC timeframes, this approach would join prostate cancer RCT’s as a very long term project. It must be mentioned that before any of these studies are undertaken, a metric of physicist performance needs to be established. Validating such a metric is a prodigious project in its own right.

At this point in the discussion, it would appear that the generation of the MOC process and its acceptance is proceeding due to the Bayesians in our midst. That MOC improves the probability of good physics practice does not seem to have been demonstrated by frequentist means. The methods of and justification for MOC appear to be informed by people’s experience with education and its value, a truly Bayesian attitude.

Conditional Probabilities

A point that has been lying just below the surface of this discussion without being baldly stated is that probabilities of an event do not exist in a vacuum. They are only valid for a given set of circumstances, the term for which is that probabilities are “conditioned”. Thus, the probability of getting heads in a coin flip is conditioned on the coin being “fair”–uniform density, aerodynamic symmetry, etc. This is written P(flip=heads | coin=fair) = 0.5 and read as “the probability that a flip yielding heads is 50% is conditioned on the state of the coin being fair.”

Let us examine the problem in this light. We have two states for which we are interested in the probabilities: a physicist’s professional practice is “good” or “bad”, i.e. P(phys=good) and P(phys=bad). Similarly there are two conditions: MOC or not. So wehave the canonical 2×2 table of conditional probabilities: P(good | MOC), P(good | ~MOC), P(bad | MOC) and P(bad | ~MOC), where “~” denotes negation. If we assume that the goal of MOC is to either improve the probability of good practice or serve as a measure of the quality of practice, we can state the following:

P(good | MOC) > P(good | ~MOC) [1]

and

P(bad | ~MOC) > P(bad | MOC), [2]

otherwise the entire MOC edifice seems to be meaningless. Another relationship is likely to be posited by the ABR which we can accept, namely:

P(good | MOC) > P(bad | MOC). [3]

This leaves some of the other relationships up for debate. For example is P(good | MOC) >, < or = P(bad | ~MOC)? Clearly, it would be a win for MOC if the former is less than the latter. However, a little reflection allows us to pin this down. Given historical events, the number of bad physicists must be relatively small, otherwise we can conclude that our status and pay is due to some collective societal blindness. The proportion of bad physicists in the pre-MOC days can reasonably be assumed to be no more than 0.1. Thus, P(good |~MOC) can be no less than 0.9 thereby resulting in the following ranking:

P(good | MOC) > P(good | ~MOC) > P(bad | ~MOC) > P(bad | MOC) [4],

which, given the above estimates, yields:

P(good | MOC) > 0.9 and P(bad | MOC) < 0.1 [5].

Bayesian Statistical Approach

One issue that needs to be addressed is whether the MOC is actually a method for improving the quality of physicists or a method of measuring the quality of a physicist. My view is that unless the ABR can reliably demonstrate that physicists do not update their skills without the pressure of MOC, we must assume that they do update them to some degree. The successful implementation of numerous new technologies into radiation oncology in the last two decades seems to be a convincing testimonial to that assumption.

In this scenario, the MOC process is a measurement designed to determine whether a physicist is of high quality. While being a quality physicist requires many skills, some of which may be difficult to determine by means of any test or MOC, we will assume that the MOC does have reasonable accuracy. It can then be considered a Bernoulli trial with an “n” of 1. To what extent can we assume that a person who passes the MOC is actually a good physicist?

This is where a Bayesian approach can help. Clearly, at this point in the MOC process, we cannot take a frequentist approach since the sample is so small. If we score a physicist on a scale of 0 to 1, with 1 being a Nobel prize-winning physicist and philanthropist, then our historical experience (as briefly noted above) can be used to develop a prior probability distribution of a physicist’s “quality score”. A beta distribution is appropriate wherein we can make sure we meet the requirements described above. A binned distribution is given in the table below which yields a probability of being a “passing” physicist with a score of 70 or more of 0.927 with approximately 7% being poor physicists.

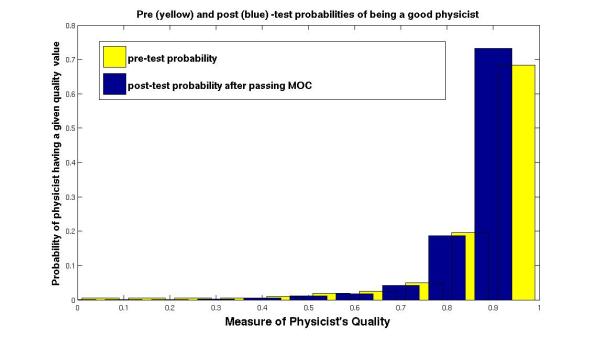
X: physicist quality Y: probability of given quality Yellow bars: pre-test probability Blue bars: post-test probability

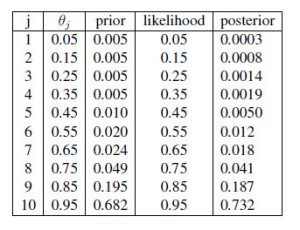
To find out how the probability distribution changes after a MOC candidate either passes or fails the MOC, we use the Bernoulli formula to calculate the likelihood of a given result for any possible value of the probability of that outcome (theta_j in the table below). Then, using Bayes’ theorem, we can calculate the posterior distribution after the test results are accounted for. The change in distributions are given for success graph above. After successfully passing the MOC, we now find that the there is a 96% chance of the physicist being of passing quality and a 4% chance that they are of poor quality. Overall, the prior and posterior distributions are pretty similar. After a failure, the distributions change a bit more dramatically. In this case, there is still a 66% chance that the physicist is of good quality (grade 0.7 or higher) and only a 34% chance that she/he is not.

An often contentious issue in the Bayesian approach is the form of the prior distribution. If one assumes complete ignorance of the distribution of physicist quality, then a success results in a probability of 51% that the physicist is good, and a failure results in a probability of 91% that they are poor. This might be used as an argument for initial certification since at that time, one might argue that the there is no knowledge of the quality of untested physicists. However, to use that same logic on practicing physicists seems to be willfully ignoring the obvious facts. One can fiddle with the exact distribution, but any realistic prior is going to give very similar results.

Conclusion

Through this simple example, we have explored two different aspects of how physicists can relate to Bayesian probability and Bayes’ theorem. In one case, there are those who believe that the MOC process improves the probability that a physicist will be of high quality. Given the lack of evidence about the results of the MOC, this highlights the role that our previous experiences and knowledge about related situations is used to color our perception of the probabilities inherent in a new situation.

In the second case, explicitly acknowledging the role that Bayes’ theorem plays in statistical reasoning, we find that while successfully undergoing MOC increases the chance of correctly identifying a good physicist, the change in probability is quite small given what we know about current physicist quality. In addition, we see that failing the MOC incorrectly identifies a physicist as being poor 2 times out of 3. These results are likely to be unexpected if one does not go through the mathematics, thereby highlighting the practical impact of the “Bayesian approach”.

Hopefully, this post has helped explain some of the uses of a Bayesian approach and will find application elsewhere. One particular application of Bayesian statistics is determining action windows for QA measurements based on what we learn as we add to our base of knowledge.